আলোর প্রতিসরণ বলতে কী বোঝায়?

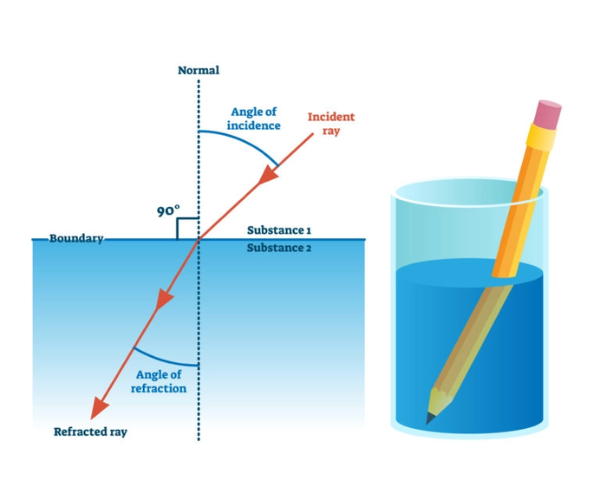
যখন আলোকরশ্মি একটি স্বচ্ছ মাধ্যম থেকে তির্যকভাবে  অন্য একটি স্বচ্ছ মাধ্যমে প্রবেশ করে, তখন মাধ্যমদ্বয়ের বিভেদতলে আলোর দিক পরিবর্তন হয়। আলোর এই দিক পরিবর্তনের ঘটনাকে আলোর প্রতিসরণ (Refraction of Light) বলে। আলোর প্রতিসরণের কারণ হলো, বিভিন্ন মাধ্যমে আলোর বেগ ভিন্ন হয়। যখন আলো ঘন মাধ্যম থেকে হালকা মাধ্যমে যায়, তখন তা অভিলম্ব থেকে দূরে সরে যায়, আর যখন হালকা মাধ্যম থেকে ঘন মাধ্যমে যায়, তখন তা অভিলম্বের দিকে বেঁকে যায়।

পূর্ণ অভ্যন্তরীণ প্রতিফলন বলতে কী বোঝায়? চিত্রসহ বর্ণনা করো।

যখন আলোকরশ্মি ঘন মাধ্যম থেকে হালকা মাধ্যমে এমনভাবে আপতিত হয় যে, প্রতিসরণ কোণের মান 90° এর চেয়ে বেশি হয়, তখন আলোকরশ্মি আর দ্বিতীয় মাধ্যমে প্রবেশ না করে প্রথম মাধ্যমেই সম্পূর্ণভাবে প্রতিফলিত হয়। আলোর এই ঘটনাকে পূর্ণ অভ্যন্তরীণ প্রতিফলন (Total Internal Reflection – TIR) বলে।

শর্তাবলি: পূর্ণ অভ্যন্তরীণ প্রতিফলন ঘটার জন্য দুটি শর্ত পূরণ হওয়া আবশ্যক:

১. আলোকরশ্মিকে অবশ্যই ঘন মাধ্যম থেকে হালকা মাধ্যমে প্রবেশ করতে হবে।

২. আপতন কোণকে অবশ্যই সংকট কোণের চেয়ে বেশি হতে হবে।

 

 

ব্যাখ্যা: যখন আপতন কোণ সংকট কোণের চেয়ে কম হয়, তখন প্রতিসরণ ঘটে। আপতন কোণ বাড়তে বাড়তে যখন সংকট কোণের সমান হয়, তখন প্রতিসরণ কোণ 90° হয় এবং প্রতিসরিত রশ্মি বিভেদতল বরাবর চলে যায়। যদি আপতন কোণ সংকট কোণের চেয়েও বেশি হয়, তখন আর প্রতিসরণ ঘটে না, বরং আলো সম্পূর্ণরূপে প্রথম মাধ্যমেই প্রতিফলিত হয়। এটিই পূর্ণ অভ্যন্তরীণ প্রতিফলন। অপটিক্যাল ফাইবার, হীরার ঔজ্জ্বল্য এবং মরীচিকার মতো ঘটনা পূর্ণ অভ্যন্তরীণ প্রতিফলনের জন্য ঘটে থাকে।

সংকট কোণ কাকে বলে?

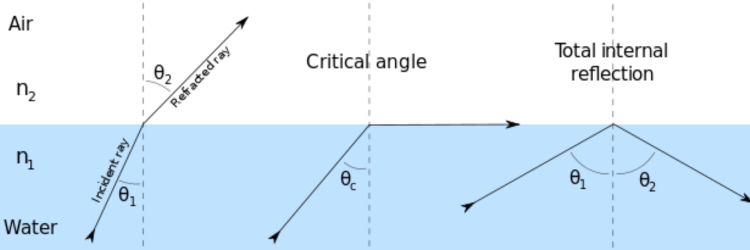
যখন আলোকরশ্মি ঘন মাধ্যম থেকে হালকা মাধ্যমে প্রবেশ করে, তখন যে আপতন কোণের জন্য প্রতিসরণ কোণ 90° হয়, সেই আপতন কোণকে সংকট কোণ (Critical Angle) বলে। একে C  দ্বারা প্রকাশ করা হয়। প্রতিটি মাধ্যম-জোড়ার জন্য একটি নির্দিষ্ট সংকট কোণ থাকে।

লেন্স কাকে বলে?

অন্তত একটি বক্রতল দ্বারা সীমাবদ্ধ দুটি স্বচ্ছ মাধ্যমের বিভেদতল দ্বারা গঠিত আলোকীয় যন্ত্রকে লেন্স (Lens) বলে। লেন্স আলোকরশ্মিকে প্রতিসরণের মাধ্যমে অভিসারী (একত্রিত) বা অপসারী (ছড়িয়ে দেওয়া) করতে পারে এবং এর মাধ্যমে প্রতিবিম্ব তৈরি করে।

লেন্স প্রধানত দুই প্রকার:

১. উত্তল লেন্স (Convex Lens):

যে লেন্সের মধ্যভাগ মোটা এবং প্রান্তভাগ সরু, তাকে উত্তল লেন্স বলে। এটি অভিসারী লেন্স নামেও পরিচিত কারণ এটি সমান্তরাল আলোক রশ্মিকে একটি বিন্দুতে একত্রিত করে।

২. অবতল লেন্স (Concave Lens):

যে লেন্সের মধ্যভাগ সরু এবং প্রান্তভাগ মোটা, তাকে অবতল লেন্স বলে। এটি অপসারী লেন্স নামেও পরিচিত কারণ এটি সমান্তরাল আলোক রশ্মিকে চারিদিকে ছড়িয়ে দেয়।

লেন্সের ক্ষমতা কাকে বলে?

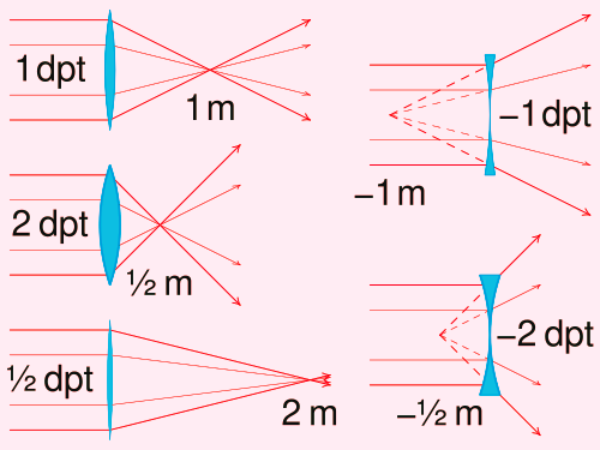
কোনো লেন্সের আলোকরশ্মিকে অভিসারী (একত্রিত) বা অপসারী (ছড়িয়ে দেওয়া) করার ক্ষমতাকে লেন্সের ক্ষমতা (Power of a Lens) বলে। লেন্সের ফোকাস দূরত্বের ব্যস্তানুপাতিক হলো এর ক্ষমতা। অর্থাৎ, ফোকাস দূরত্ব যত কম হয়, লেন্সের ক্ষমতা তত বেশি হয়।

লেন্সের ক্ষমতা (P) ফোকাস দূরত্ব (f) এর সাথে সম্পর্কিত:

P= 1 \ f 

এখানে, f মিটার এককে প্রকাশিত হয়। লেন্সের ক্ষমতার একক হলো ডায়াপ্টার (Dioptre), যাকে D দ্বারা প্রকাশ করা হয়।

উত্তল লেন্সের ক্ষমতা ধনাত্মক এবং অবতল লেন্সের ক্ষমতা ঋণাত্মক হয়।

আলোর প্রতিসরণের সূত্রগুলো লেখ।

আলোর প্রতিসরণের দুটি সূত্র রয়েছে:

১. প্রথম সূত্র: আপতিত রশ্মি, প্রতিসরিত রশ্মি এবং আপতন বিন্দুতে দুই মাধ্যমের বিভেদতলের ওপর অঙ্কিত অভিলম্ব সর্বদা একই সমতলে থাকে।

২. দ্বিতীয় সূত্র (স্নেলের সূত্র): একজোড়া নির্দিষ্ট মাধ্যম এবং একটি নির্দিষ্ট রঙের আলোর জন্য, আপতন কোণের সাইন এবং প্রতিসরণ কোণের সাইন এর অনুপাত সর্বদা একটি ধ্রুবক হয়। এই ধ্রুবককে দ্বিতীয় মাধ্যমের সাপেক্ষে প্রথম মাধ্যমের প্রতিসরণাঙ্ক বলে।

গাণিতিকভাবে: Sini \ sinr ​= ধ্রুবক =μ

যেখানে i হলো আপতন কোণ, r হলো প্রতিসরণ কোণ এবং μ (মিউ) হলো প্রতিসরণাঙ্ক।

প্রতিসরণাঙ্ক এবং সংকট কোণের মাঝে সম্পর্ক স্থাপন করো।

আমরা জানি, সংকট কোণ (C) হলো ঘন মাধ্যম থেকে হালকা মাধ্যমে আলোর প্রতিসরণের সময় আপতন কোণের সেই নির্দিষ্ট মান, যার জন্য প্রতিসরণ কোণ (r) 90° হয়।

স্নেলের সূত্র অনুযায়ী,

\[
n_1 \sin i = n_2 \sin r
\]

যেখানে \( n_1 \) ঘন মাধ্যমের প্রতিসরণাঙ্ক এবং \( n_2 \) হালকা মাধ্যমের প্রতিসরণাঙ্ক।

সংকট কোণের ক্ষেত্রে, \( i = C \) এবং \( r = 90^\circ \)।

সুতরাং,

\[
n_1 \sin C = n_2 \sin 90^\circ
\]

বা,

\[
n_1 \sin C = n_2 \times 1 \quad \text{[কারণ } \sin 90^\circ = 1\text{]}
\]

বা,

\[
n_1 \sin C = n_2
\]

বা,

\[
\sin C = \frac{n_2}{n_1}
\]

বা,

\[
\sin C = \frac{1}{n_1} \quad \text{[যদি হালকা মাধ্যমটি বায়ু বা শূন্যস্থান হয়, তবে } n_2 = 1\text{]}
\]

অর্থাৎ, সংকট কোণের সাইন মান ঘন মাধ্যমের প্রতিসরণাঙ্কের ব্যস্তানুপাতিক। এটিই প্রতিসরণাঙ্ক এবং সংকট কোণের মধ্যকার সম্পর্ক।

ন্যূনতম বিচ্যুতির রাশিমালা নির্ণয় করো ।

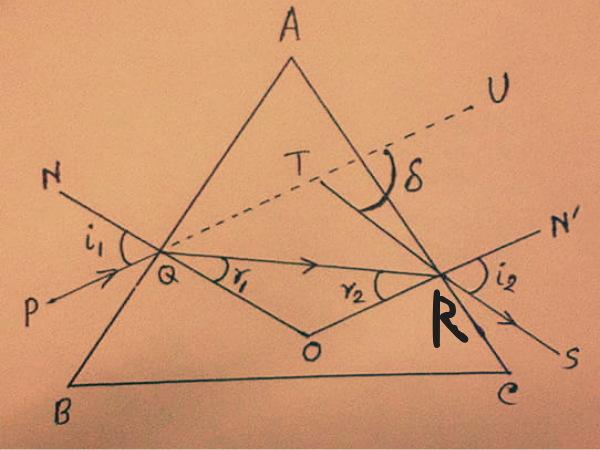
একটি প্রিজমের মধ্য দিয়ে আলোকরশ্মি যাওয়ার সময় দুইবার প্রতিসরণের কারণে তার মূল পথ থেকে বিচ্যুত হয়।
এই বিচ্যুতি কোণকে বিচ্যুতি কোণ ( \( \delta \) ) বলে।
প্রিজমের একটি নির্দিষ্ট আপতন কোণের জন্য এই বিচ্যুতি কোণের মান সর্বনিম্ন হয়, যাকে ন্যূনতম বিচ্যুতি কোণ ( \( m \) ) বলে।

একটি প্রিজমের মধ্য দিয়ে আলোর প্রতিসরণের ক্ষেত্রে, ন্যূনতম বিচ্যুতির শর্তে:

– আলোক রশ্মিটি প্রিজমের ভিতরে ভূমির সমান্তরালভাবে চলে।
– আপতন কোণ \( i_1 \) এবং নির্গমন কোণ \( i_2 \) সমান হয় ( \( i_1 = i_2 = i \) )।
– প্রথম প্রতিসরণ কোণ \( r_1 \) এবং দ্বিতীয় প্রতিসরণ কোণ \( r_2 \) সমান হয় ( \( r_1 = r_2 = r \) )।

ধরা যাক, ABC একটি কাঁচ প্রিজমের প্রধান ছেদ,
AB এবং AC প্রতিসরণ তল, BC ভূমি, A প্রিজম কোণ।

PQRS আলোক রশ্মির গতিপথ নির্দেশ করে।
PQ রশ্মি AB তলের Q বিন্দুতে আপতিত হয়ে NQO অভিলম্বের দিকে বেঁকে যায়
এবং QR পথে AC তলের R বিন্দুতে আপতিত হয়ে N’RO হতে দূরে সরে RS পথে নির্গত হয়।
PQ কে U পর্যন্ত বর্ধিত করলে এবং RS কে পিছনের দিকে বর্ধিত করলে তারা T বিন্দুতে মিলিত হয়,
যেখানে \( \delta \) বিচ্যুতি কোণ নির্দেশ করে।

চিত্র হতে, \( \triangle TQR \) এর বহিস্থ কোণ:

\[
\delta = i_1 – r_1 + i_2 – r_2
\]

বা,

\[
\delta = i_1 + i_2 – (r_1 + r_2) \tag{1}
\]

আবার, \( \triangle OQR \) হতে,

\[
r_1 + r_2 + \angle O = 180^\circ \tag{2}
\]

এবং, চতুর্ভুজ AQOR এ \( \angle AQO \) ও \( \angle ARO \) সমকোণ হওয়ায়,

\[
A + \angle O = 180^\circ \tag{3}
\]

(2) ও (3) তুলনা করে,

\[
r_1 + r_2 = A \tag{4}
\]

(4) এর মান (1)-এ বসিয়ে পাই,

\[
\delta = i_1 + i_2 – A \tag{5}
\]

ইহাই বিচ্যুতি রাশিমালা।

এখন, ন্যূনতম বিচ্যুতির শর্ত অনুযায়ী, \( i_1 = i_2 = i \), এবং \( r_1 = r_2 = r \)

(4) থেকে,

\[
r_1 + r_1 = A \Rightarrow 2r = A \Rightarrow r = \frac{A}{2}
\]

(5) থেকে,

\[
m = i + i – A = 2i – A \Rightarrow i = \frac{m + A}{2}
\]

আমরা জানি, প্রিজমের প্রতিসরাঙ্ক:

\[
\mu = \frac{\sin i}{\sin r}
\]

মানে,

\[
\mu = \frac{\sin \left( \frac{m + A}{2} \right)}{\sin \left( \frac{A}{2} \right)}
\]

 

🎯 **এই রাশিমালাটিই প্রমাণ করে যে**,
ন্যূনতম বিচ্যুতির শর্তে একটি প্রিজমের প্রতিসরাঙ্ক,

\[
\boxed{
\mu = \frac{\sin \left( \frac{m + A}{2} \right)}{\sin \left( \frac{A}{2} \right)}
}
\]

লেন্সের ক্ষেত্রে দেখাও যে, 1\u+1\v=1\f

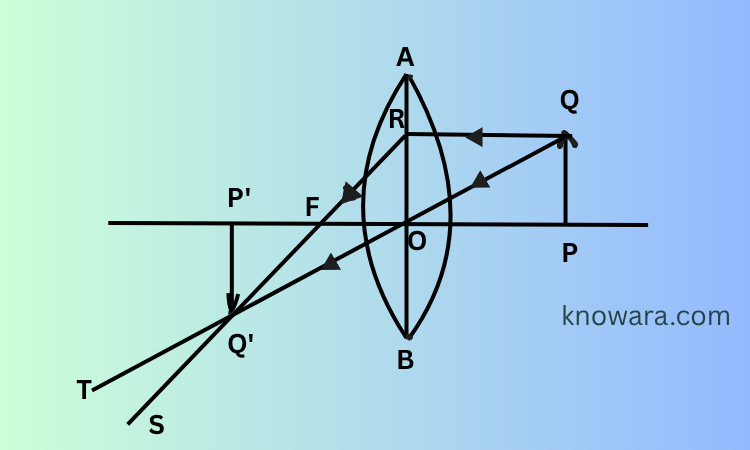
ধরা যাক, AB একটি উত্তল লেন্সের প্রধান ছেদ, O আলোক কেন্দ্র এবং F প্রধান ফোকাস।
প্রধান অক্ষে Q একটি বস্তু রাখা হয়েছে।

Q থেকে একটি আলোক রশ্মি QR পথে প্রধান অক্ষের সমান্তরালভাবে লেন্সের R বিন্দুতে আপতিত হয়।
প্রতিসরণের পর এটি লেন্সের প্রধান ফোকাস F দিয়ে যায়।

Q থেকে আরেকটি আলোক রশ্মি QO পথে আলোক কেন্দ্র O দিয়ে যায় এবং কোনো বিচ্যুতি ছাড়াই সোজা চলে যায়।
এই দুটি প্রতিসরিত রশ্মি Q’ বিন্দুতে মিলিত হয়।

Q′ থেকে প্রধান অক্ষের ওপর লম্ব \( P′Q′ \) হলো \( PQ \) বস্তুর বাস্তব, উল্টো প্রতিবিম্ব।

**প্রমাণঃ**

\( \triangle POQ \) এবং \( \triangle P′OQ′ \) সদৃশকোণী হওয়ায়,

\[
\frac{PQ}{P′Q′} = \frac{OP}{OP′} \tag{1}
\]

আবার, \( \triangle ROF \) এবং \( \triangle P′Q′F \) সদৃশকোণী হওয়ায়,

\[
\frac{OR}{P′Q′} = \frac{OF}{P′F}
\]

বা,

\[
\frac{PQ}{P′Q′} = \frac{OF}{OP′ – OF} \quad \text{[কারণ } OR = PQ \text{ এবং } P′F = OP′ – OF ]
\]

সুতরাং,

\[
\frac{OP}{OP′} = \frac{OF}{OP′ – OF}
\]

এখন, প্রচলিত চিহ্ন অনুযায়ী, \( OP = u \), \( OP′ = v \), এবং \( OF = f \)।
তাহলে উপরের সমীকরণে বসালে পাই,

\[
\frac{u}{v} = \frac{f}{v – f}
\]

ক্রস মাল্টিপ্লাই করে পাই,

\[
u(v – f) = vf
\]

বা,

\[
uv – uf = vf
\]

এখন উভয় পক্ষকে \( uvf \) দ্বারা ভাগ করি:

\[
\frac{uv}{uvf} – \frac{uf}{uvf} = \frac{vf}{uvf}
\]

সরলীকরণে,

\[
\frac{1}{f} – \frac{1}{v} = \frac{1}{u}
\]

বা,

\[
\frac{1}{u} + \frac{1}{v} = \frac{1}{f} \quad \text{(প্রমাণিত)}
\]